Predicting household poverty in Latin America, Part I: Re-splitting the CRHP dataset

The core data fields

The main ‘target’ variable in this dataset is a poverty-level classification with four values: “extreme poverty”, “moderate poverty”, “vulnerable”, and “non-vulnerable”.

There are two variables that serve as identifiers–‘Id’ and ‘idhogar’, a unique individual-level identifier and an identifier for which individuals belong to the same household, respectively. An additional variable, ‘parentesco1’ is a dummy that indicates whether a given individual is the head of a household.

Re-splitting the data

The main problem with this dataset is that the available test set does not include the target variable. This was done so that, separately, competing teams could build their models and make their predictions, and organizers could see which teams had the most accurate predictions and select the competition winners. The competition concluded in September of 2018, and the organizers have, at present, still not released the full test set including the target variable, and thus, this data is unusable to us for supervised learning approaches.

The good news is that the training set that is available still contains over 9,500 observations and the target variable, which will allow us to train some basic machine learning algorithms after we re-split it into new training and test sets.

The prime consideration when re-splitting this data is how to manage the two identifiers–‘Id’ and ‘idhogar’. As the goal of the original Kaggle competition was to predict household poverty levels, the ‘idhogar’ grouping is quite important, and indeed the original Kaggle dataset does not divide any households between training and test sets, but rather, keeps the households together on their respective partitions, which makes sense.

While it is quite simple to partition the original training data into new training and test sets using the built-in functions in caret or caTools, neither of these packages currently includes an easy way to partition based on a target variable, while preserving entire household groupings in a balanced way between training and test sets.

In the end, in order to do a proper blocking of the ‘idhogar’ variable and ensure that households were not randomly divided over both the new training and test sets, I performed the data partitioning manually, using dplyr to do repeated random splits of the data in such a way as to preserve the household groupings, and then identifying the seed used where the random split resulted in the most balanced Target distribution in both the new training and test set.

First, we can have a look a the distribution of the ‘Target’ variable in the original CRHP training set:

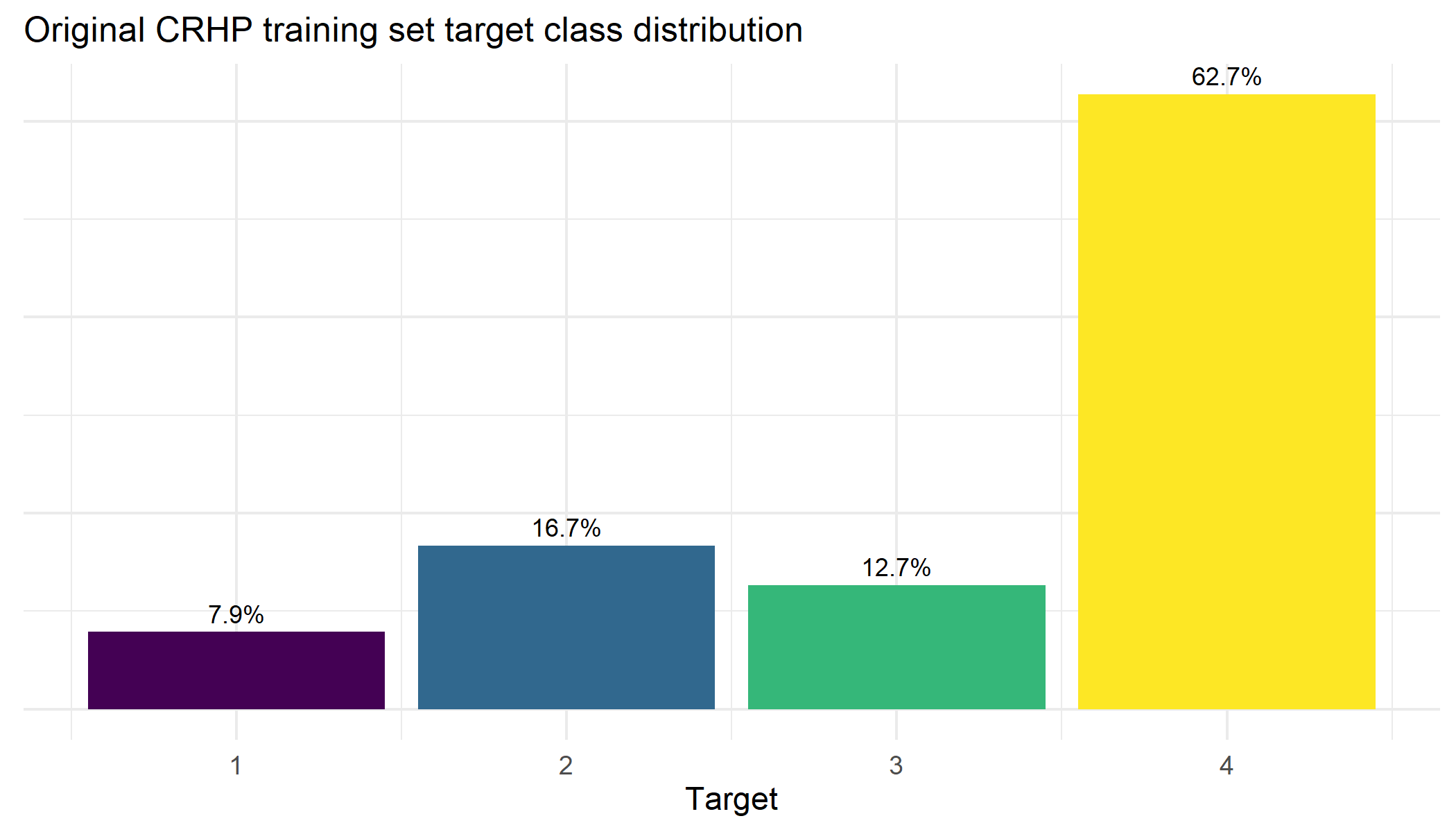
Next, I did 1000 random splits, and then looked for the seed where the frequencies of the different target variable classes between the two sets were the most similar. We can see in the plot below that the balance of the ‘target’ variable classes in our final re-split data is both very well balanced and also matches quite nicely with the original CHRP training set:

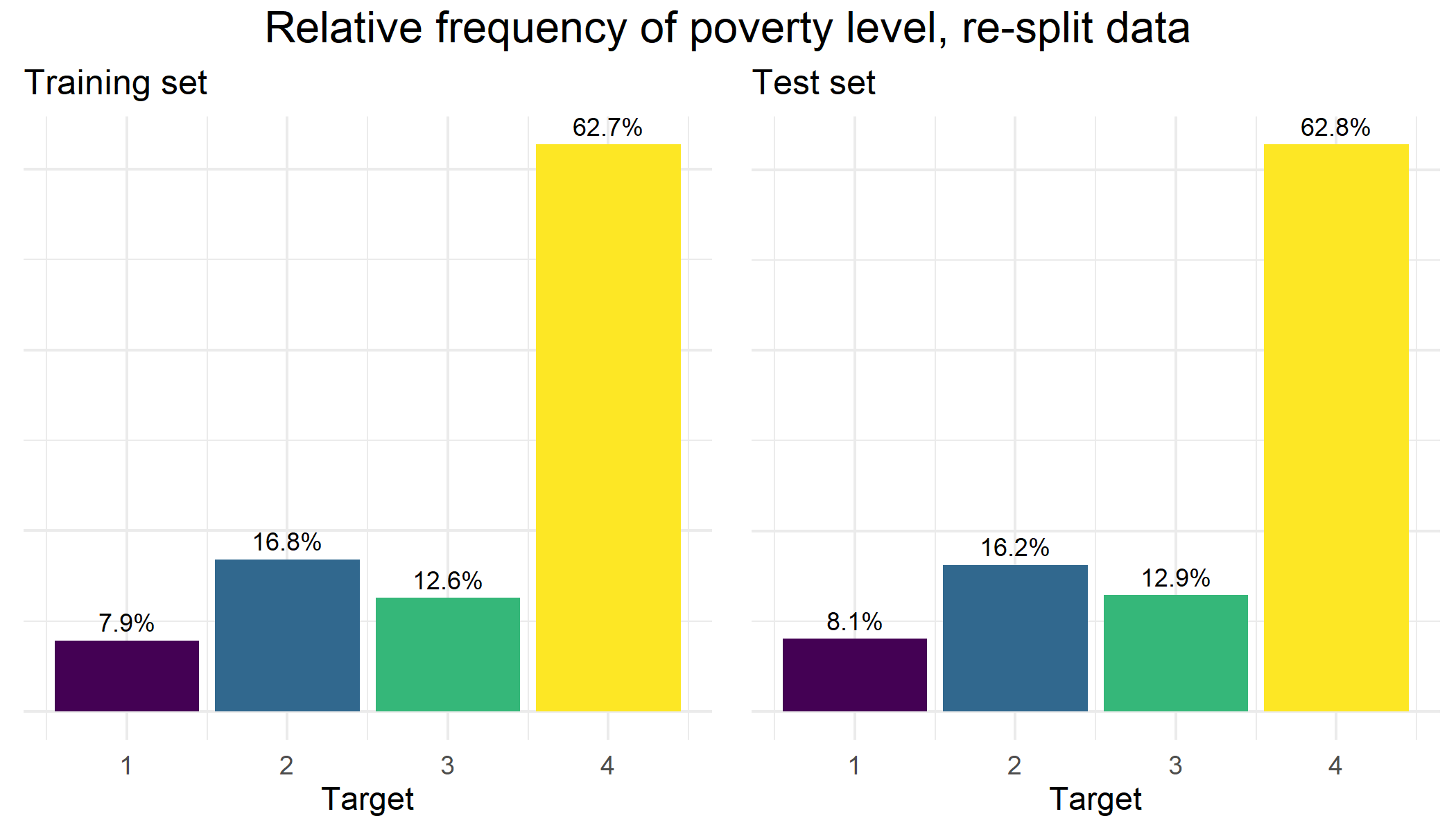
While I do not exploit the household grouping information for this particular analysis, our newly split data captures all of this information and can be used for future projects. Visit my github site to download the CRHP re-split dataset.

Similarly, I also have an Rmarkdown document that contains further analysis on the re-split CRHP data, where I show that the proportion of unique households and the size of households between both sets is also well-balanced.

Missing values

We can check to see what percentage of the dataset is made up of missing values:

# calculate percentage of data that is NA
round(sum(is.na(train))/sum(!is.na(train)) * 100, 2)

## [1] 1.64

While there are some missing values in our data, the good news is that their percentage is fairly low at 1.66%.

Next we can calculate the percentage of missing values by column to see if there are some variables that are more problematic than others:

na_vars <- colMeans(is.na(train))
na_vars <- na_vars[na_vars > 0]
na_vars <- sort(na_vars, decreasing=TRUE)
na_vars

##      rez_esc        v18q1         v2a1     meaneduc    SQBmeaned 
## 0.8276898941 0.7665054255 0.7169564649 0.0006536802 0.0006536802

Luckily, we can see that there are only five columns in the entire dataset that have missing values, and only three of these have NAs of any meaningful percentage. These variables are:

• rez_esc, Years behind in school
• v18q1, number of tablets household owns
• v2a1, Monthly rent payment
• meaneduc, average years of education for adults (18+)
• SQBmeaned, square of the mean years of education of adults (>=18) in the household

Ordinarily, it would be good to dig deeper into these variables to understand why they have so many NAs and see if we can fill them in, but again, as our main interest is fitting multiple models to see how they compare, we will just drop these variables from our analysis entirely as they are reasonably approximated by other variables in the dataset. Similarly, as we continue pre-processing our data, we will just drop other potentially problematic variables straight away rather than spending extra time during this stage to re-work them.

And finally, because we will eventually have to drop these same variables later in our test est, we will create a vector to store the names of all variables we eliminate as we go along:

library(dplyr)

# store names of NA variables to drop
drop_cols <- train %>% select(rez_esc, v2a1, v18q1, meaneduc, SQBmeaned) %>% names() %>% as_tibble()

# drop NA values
train_filtered <- train[ ,!names(train) %in% drop_cols$value]

dim(train_filtered)

## [1] 7649  138

Zero-variance predictors

Next, we can continue to pare down our feature set by looking for zero-variance or near-zero-variance predictors. As described in the caretdocumentation:

In some situations, the data generating mechanism can create predictors that only have a single unique value (i.e. a “zero-variance predictor”). For many models (excluding tree-based models), this may cause the model to crash or the fit to be unstable. Similarly, predictors might have only a handful of unique values that occur with very low frequencies…

The concern here that these predictors may become zero-variance predictors when the data are split into cross-validation/bootstrap sub-samples or that a few samples may have an undue influence on the model. These “near-zero-variance” predictors may need to be identified and eliminated prior to modeling.

For this, we can use the nearZeroVar function in caret that makes this task fairly simple:

library(caret)
# identify NZV predictors
nzv <- nearZeroVar(train_filtered)

# show names of NZV predictors
train_filtered[, nzv] %>% names()

##  [1] "hacdor"          "hacapo"          "v14a"           
##  [4] "refrig"          "pareddes"        "paredzinc"      
##  [7] "paredfibras"     "paredother"      "pisoother"      
## [10] "pisonatur"       "pisonotiene"     "techozinc"      
## [13] "techoentrepiso"  "techocane"       "techootro"      
## [16] "abastaguadentro" "abastaguafuera"  "abastaguano"    
## [19] "planpri"         "noelec"          "sanitario1"     
## [22] "sanitario5"      "sanitario6"      "energcocinar1"  
## [25] "energcocinar4"   "elimbasu2"       "elimbasu4"      
## [28] "elimbasu5"       "elimbasu6"       "estadocivil4"   
## [31] "estadocivil6"    "parentesco4"     "parentesco5"    
## [34] "parentesco7"     "parentesco8"     "parentesco9"    
## [37] "parentesco10"    "parentesco11"    "parentesco12"   
## [40] "instlevel6"      "instlevel7"      "instlevel9"     
## [43] "tipovivi4"       "mobilephone"

Again, ideally, we would dig into these variables a bit more to understand what is going on here, but to keep this simple, and as our main identification and outcome variables are not included in this list, we will just drop all 44 of these nzv predictors outright. The procedure is as before:

# store names of NZV variables to drop
drop_cols <- train_filtered[, nzv] %>% names() %>% as_tibble() %>% rbind(drop_cols, .)

# drop NZV variables
train_filtered <- train_filtered[, -nzv]

dim(train_filtered)

## [1] 7649   94

Correlated predictors

To weed out any redundant variables we can also create a correlation matrix based on our filtered data and remove any variables that are too highly correlated. In order to use the cor function our data needs to be composed entirely of numeric values, which in our case it is not (i.e. our ID variables are character strings).

We can run the following code to convert our train_filtered data into a numeric matrix that will be accepted by the cor function, and then run our correlation analysis to identify highly redundant variables:

# Convert data.frame to integer-class matrix
l <- lapply(train_filtered, function(X) as.numeric(factor(X, levels=unique(X))))
m <- as.matrix(data.frame(l))

# Identify pairs of perfectly correlated columns
M <- (cor(m,m) == 1)

M[lower.tri(M, diag=TRUE)] <- FALSE

## Extract the names of the redundant columns
colnames(M)[colSums(M) > 0]

##  [1] "hhsize"          "female"          "hogar_total"    
##  [4] "area2"           "SQBescolari"     "SQBage"         
##  [7] "SQBhogar_total"  "SQBedjefe"       "SQBovercrowding"
## [10] "SQBdependency"   "agesq"

Looking at these results, they make intuitive sense. There are other variables besides hhsizeand hogar_total that capture how many people live in a household. female is a dummy variable complemented by the male variable which has the same information. The rest of these variables are squared terms of existing variables. We can therefore drop all of these from train_filtered and move on to the next step.

# Store names of perfectly correlated columns
drop_cols <- colnames(M)[colSums(M) > 0] %>% as_tibble() %>% rbind(drop_cols, .)

# Drop perfectly correlated columns
train_filtered <-train_filtered[ ,!names(train_filtered) %in% drop_cols$value]

dim(train_filtered)

## [1] 7649   83

Linear Combinations

The caret package includes the findLinearCombos function, a simple solution for identifying and removing linearly dependent variables from our dataset. This will further help us reduce dimensionality and improve the performance of our model.

# re-run previous code to convert latest train_filtered back to matrix form
l <- lapply(train_filtered, function(X) as.numeric(factor(X, levels=unique(X))))
m <- as.matrix(data.frame(l))

# find columns to eliminate linear dependencies
comboInfo <- findLinearCombos(m)

# print column names to remove
colnames(m)[comboInfo$remove]

## [1] "etecho3"      "eviv3"        "lugar6"       "SQBhogar_nin"

When we look up the descriptions of these four variables, we can see that they all belong to sets of dummy variables that have not had one dropped, so they would have perfect multicolinearity if not removed. We will add these four names to our list, and then drop them from train_filtered:

# Store names of linearly dependent variables
drop_cols <- colnames(m)[comboInfo$remove] %>% as_tibble() %>% rbind(drop_cols, .)

# Drop linearly dependent variables
train_filtered <-train_filtered[ ,!names(train_filtered) %in% drop_cols$value]

dim(train_filtered)

## [1] 7649   79

dependency

To inspect the dependency variable, we select the relevant columns from its calculation and have a look with the following code:

dep_check <- train_filtered %>% select(Id, idhogar, tamhog, tamviv, age, dependency)

head(dep_check, 10)

I’m only showing the head of this check for illustrative purposes, but going through the entire subset we just took, the calculations still don’t make sense to me with regards to why a value takes a number, a “yes”, or a “no”, so I will drop the column from our training set for the time being.

drop_cols <- train_filtered %>% select(dependency) %>% names() %>% as_tibble() %>% rbind(drop_cols, .)

# drop NA values
train_filtered <- train_filtered[ ,!names(train_filtered) %in% drop_cols$value]

dim(train_filtered)

## [1] 7649   78

edjefe and edjefa

Similar to what we did above, we can also subset our data to do a visual inspection of these two variables:

edjef_check <- train_filtered %>%  select(Id, idhogar, parentesco1, male, escolari , edjefe, edjefa)

head(edjef_check, 10)

Here, it seems that each variable just takes on the value of the escolari variable for whoever is identified as the head of household (parentesco1) for any given group with the same idhogar identifier. When escolari is 1 year, it is being converted to a “yes”, and when it is 0 years, it is being converted to a “no”. We can easily fix this by just converting all yes/no values to 1/0 with the following code:

# replace no/yes with 0/1, convert columns to numeric
train_filtered$edjefe <- as.numeric(ifelse(train_filtered$edjefe == "no", 0, ifelse(train_filtered$edjefe == "yes", 1, train_filtered$edjefe)))
train_filtered$edjefa <- as.numeric(ifelse(train_filtered$edjefa == "no", 0, ifelse(train_filtered$edjefa == "yes", 1, train_filtered$edjefa)))