Refugee supply shocks and the Swiss labor market, Part II: Expanding the sample, analyzing alternative outcomes

Background

In Part I of this analysis, I use the region-skill cell analysis approach developed by Borjas¹ to examine the labor market impact of the sudden spike in immigration of refugees from the Balkan states to Switzerland in the 1990s. In a similar analysis by Borjas and Monras² that also uses the census data available through IPUMS International, the Balkan refugee supply shock of the 1990s was shown to have a significantly negative effect on the employment rate of a selection of European countries, one of which, included Switzerland.

For this analysis the identification strategy relies on the fact that the sudden spike in asylum flows to Europe and Switzerland are captured neatly in the decennial census data from 1990 and 2000, as can be inferred from the figure below³. More generally, refugee migration is argued to be exogenous to the domestic labor market in terms of its timing, skill composition and quantity of labor supplied and thus allows us to study the impact of migration on our outcomes of interest.

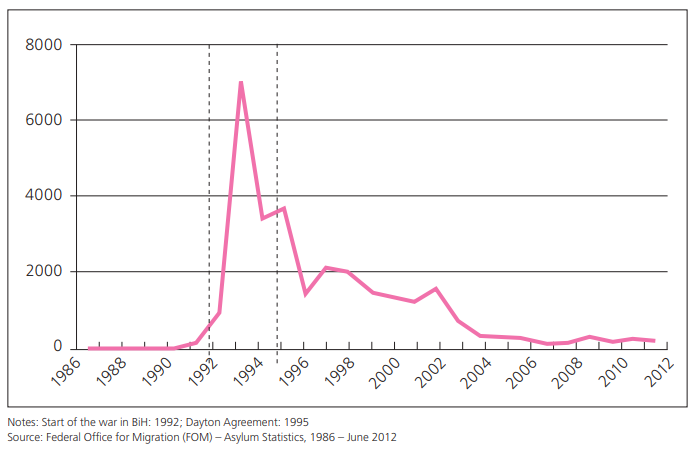
In my previous analysis, I use a fairly restricted sample of prime-age working males, mimicking the original Borjas approach. It has been argued by many others, notably Clemens in this Vox article, and even more recently by Banarjee and Duflo⁴, that while the data is very noisy, there are not necessarily any good economic reasons for excluding non-prime age workers and women from the sample.

With that in mind, in this follow-up post, I wanted to see what would happened to our estimates once I expanded the sample to include all working age adults, both male and female. Furthermore, as our dataset includes variables that capture other elements of the labor market–namely, contract types and labor force participation–I also have a look to see if the Balkan shock has had any impact on these outcomes as well. Given that my original analysis of the restricted sample found no significant effect of the Balkan refugee shock on the Swiss unemployment rate, I anticipate largely the same results in this follow-up.

Empirical specification

The specification for this analysis has not changed much since the first post, other than I add a control for women, given our expanded sample. I, again, use the region-skill cell approach, which has the advantage of being a national-level approach that accounts for the uneven distribution of immigrants across different local labor markets, as well as the movement of native workers as they adjust in response (and thus, re-balance the national market).

Practically, this approach entails dividing the national labor market into a number of different “cells” that are defined by a regional unit and unit capturing the skill levels of the workers. Given sufficient data, the cells can be refined to capture an additional \(N\)-dimensions (e.g. age groups, occupation types, etc.).

For our purposes, we define our cells using the Swiss cantons (25) and the highest education-level completed by the individual (3 levels), giving us a a total of 75 region-skill cells.

Next, the change in the composition of the labor force represented by each cell due to Balkan migration is calculated, and this change–or “shock”–in the relative supply of foreign workers is used to estimate the impact of migration on native labor market outcomes.

Formally, the empirical specification used in this analysis takes the form:

\[ \Delta Y_{r,s} = \beta_1 \text{Shock}_{r,s} + \beta_2 \Delta \text{NativeSupply}_{r,s}+ \beta_3 \Delta \text{ShareFemale}_{r,s} + \theta_r + \theta_s + \epsilon_{r,s} \]

Where our regressor of interest, the relative supply shock of Balkan refugees (\(Shock_{r,s}\)), is equal to the percent increase in the number of workers due to the entry of refugees into the given cell (\(r,s\)) in the year 2000. Additionally, we add a control for the change in native labor supply between the two periods (\(\Delta \text{NativeSupply}\)), as well as a control for the change in the share of female workers (\(\Delta \text{ShareFemale}\)).

As our data is a pooled cross-section from multiple years, our OLS estimates will be biased unless we correct for time invariant characteristics that could affect our dependent and independent variables ⁵. To address this issue, we include \(\theta_r\) and \(\theta_s\), which control for region and skill fixed-effects in our data.

To assess the impact of the refugee shock on the labor market, we look at three different dependent variables–the change in the native unemployment rate, the change in the share of native salaried workers, and the change in the native labor force participation rate. Among our three dependent variables, the unemployment rate should take a different sign than the share of salaried workers and the labor force participation rate. For estimations of the latter two, we would expect the signs of our regressor of interest to flip to negative.

Our intuition on this point comes from basic neo-classic economic theory, which states that:

The laws of supply and demand have unambiguous implications for how immigration should affect labor market conditions in the short run. The shift in supply lowers the real wage of competing native workers. Further, as long as the native supply curve is upward sloping, immigration should also reduce the amount of labor supplied by the native workforce [Borjas 2003].

Slicing up the sample

As already mentioned, I wanted to see how much the results were affected by the sample restrictions, so for this analysis, I created three different sub-samples of the Swiss census data: prime-working age males only (Ages 15-54), all working age males (Ages 15+), and all working age male and females (Ages 15+). In keeping with the literature, I use educational attainment level to proxy for worker skill-level, with the idea that workers with similar skill-levels in the same regional markets would compete for jobs.

When we look at the educational distribution for native workers, we can see that the majority of the sample has completed secondary schooling, and there is a slightly higher number of those with post-secondary education as opposed to only primary education. Glancing at Figure 1 below, we can see that, no matter how we slice the sample, the relative proportions of this educational attainment distribution remains the same across all samples.

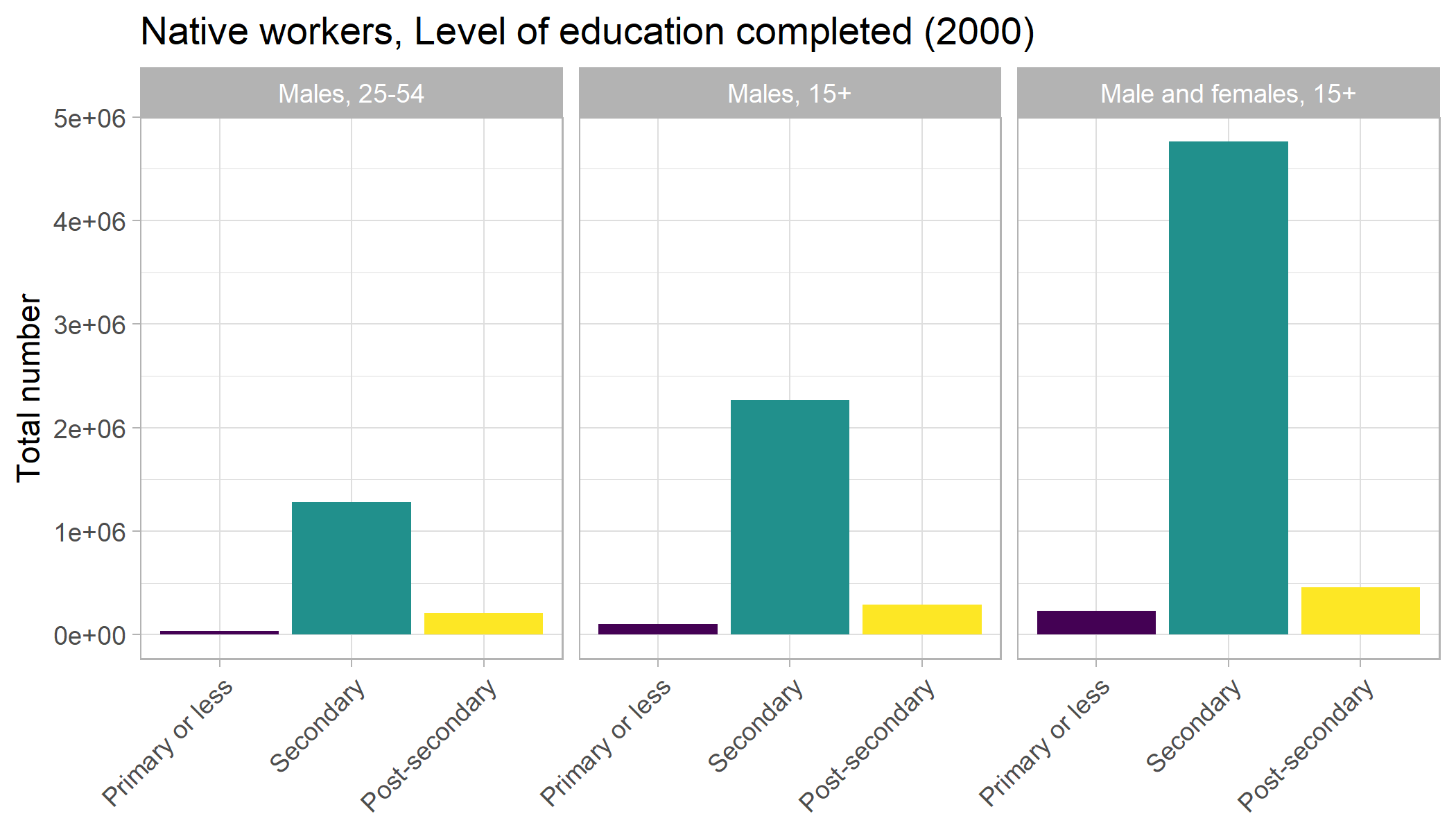
Figure 1

On the other hand, for the Balkan population, the picture changes considerably depending on which sample we use. As can be seen in Figure 2, when we restrict our sample to only prime-working age males, the bulk of the population has only completed primary education or less, but as we relax this sample restriction the educational attainment distribution changes considerably. In our full sample of all working age male and females, the bulk of the Balkan population has completed secondary education. This is similar to the native workforce, though the split between secondary and primary education for the Balkan workers is a bit closer than that found for natives in the same sample.

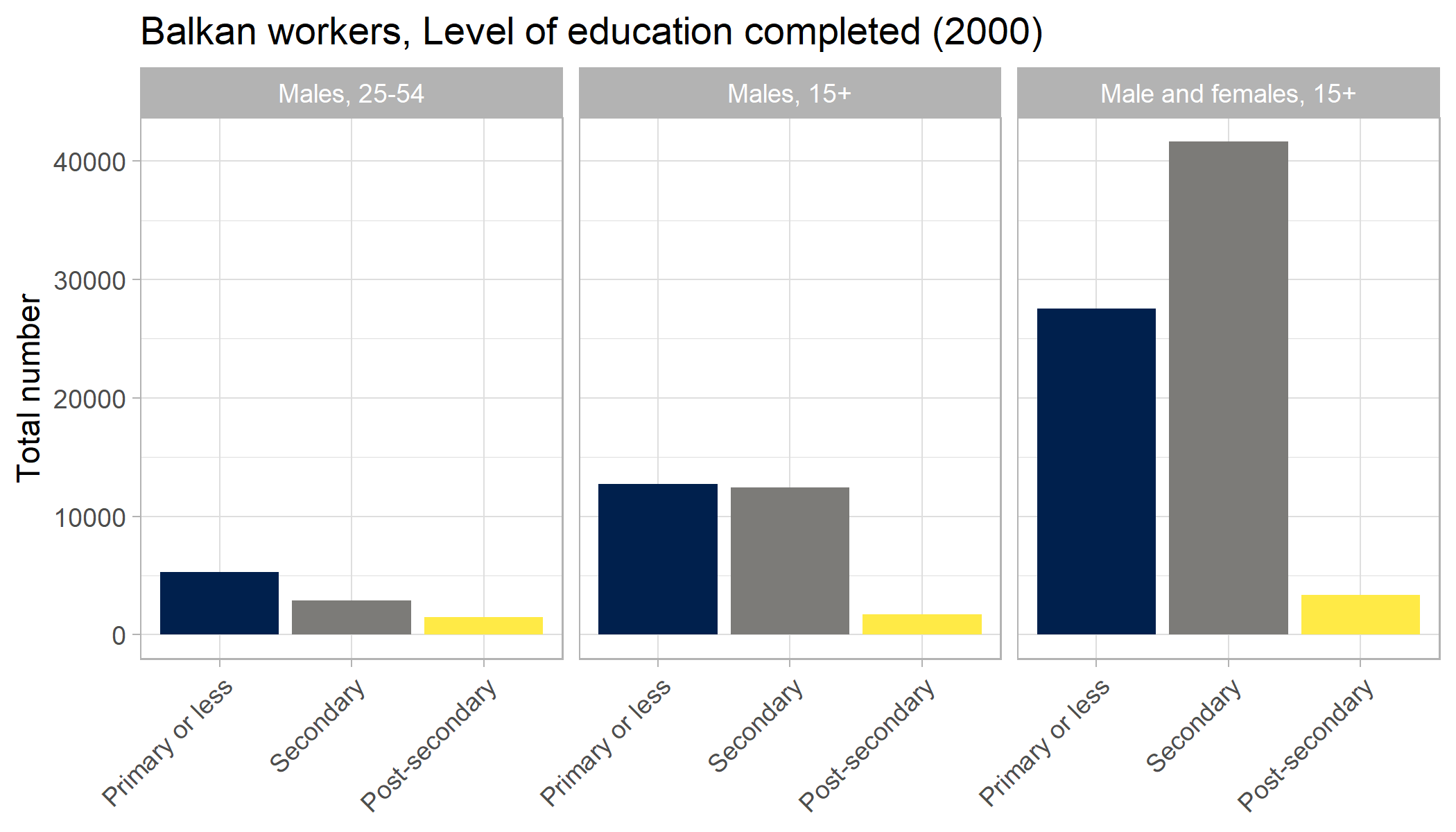
Figure 2

For the rest of this analysis, I will only be reporting the results using the full sample of male and females of working age, though it should be noted that regression results using all three samples had the same signs and significance levels.

Estimating the supply shock

The first thing to note here is that, while there certainly was a dramatic spike in the flows of migrants from the Balkan states entering Switzerland in the 1990s, as a percentage of the total workforce, this “shock” is still relatively modest. In Figure 3 below, we can see that for the full sample of male and female workers, the Balkan population made up 2.29% and 3.59% of the Swiss labor force in 1990 and 2000 respectively.

[Note: Even when using the restricted sample of prime-working age males, the share of Balkan workers is only 4.04% and 4.71% over both years.]

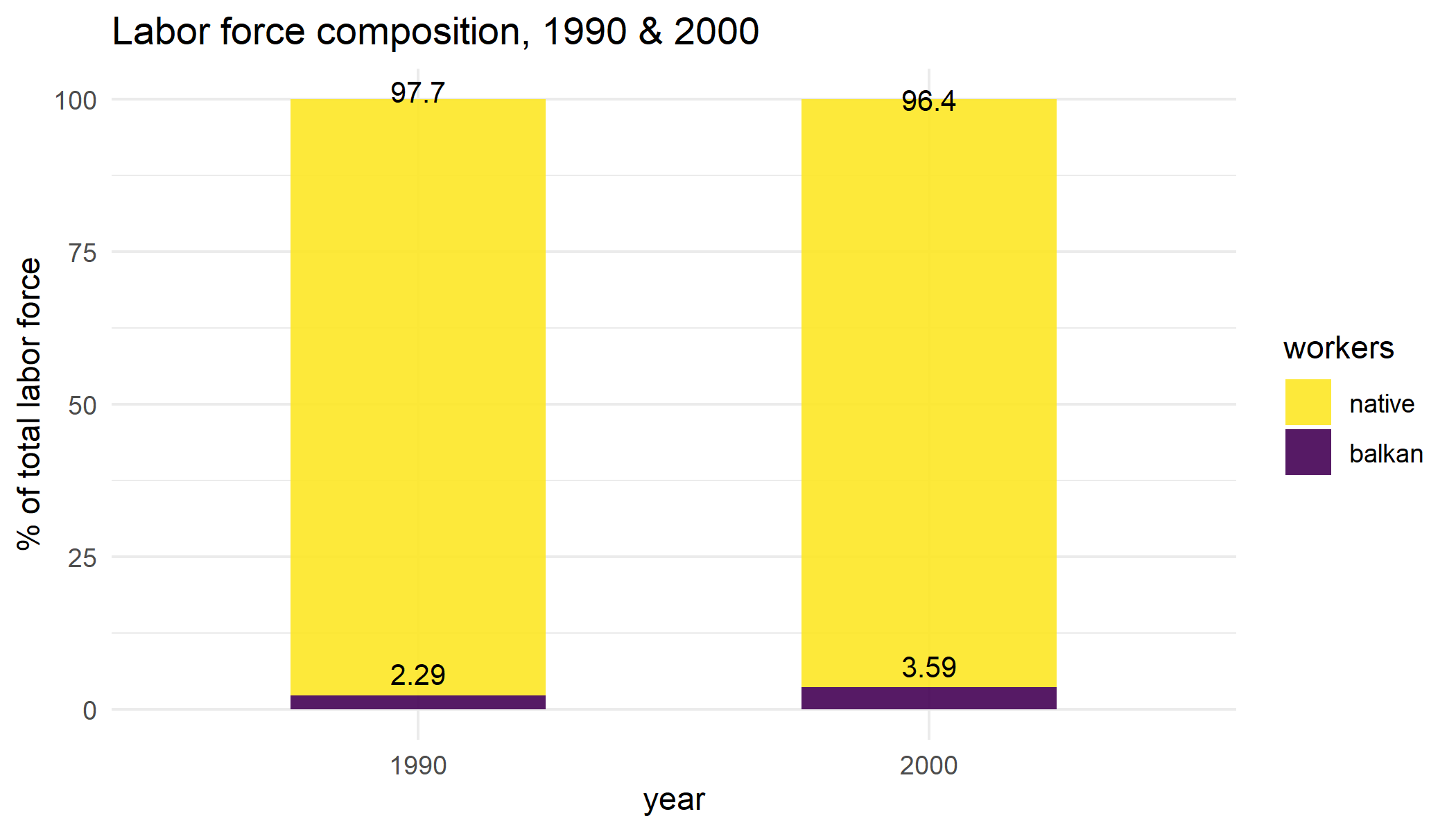
Figure 3

With regards to where these shocks were felt the most, we can see that, while the variation is modest, not all of the cantons in Switzerland were affected the same way–as we would expect. In the map below, we can see that majority of cantons only experienced relatively light “shocks”, ranging between 1 to 2%, and that the biggest impacts tend to have occurred in the central and northeastern parts of the country.

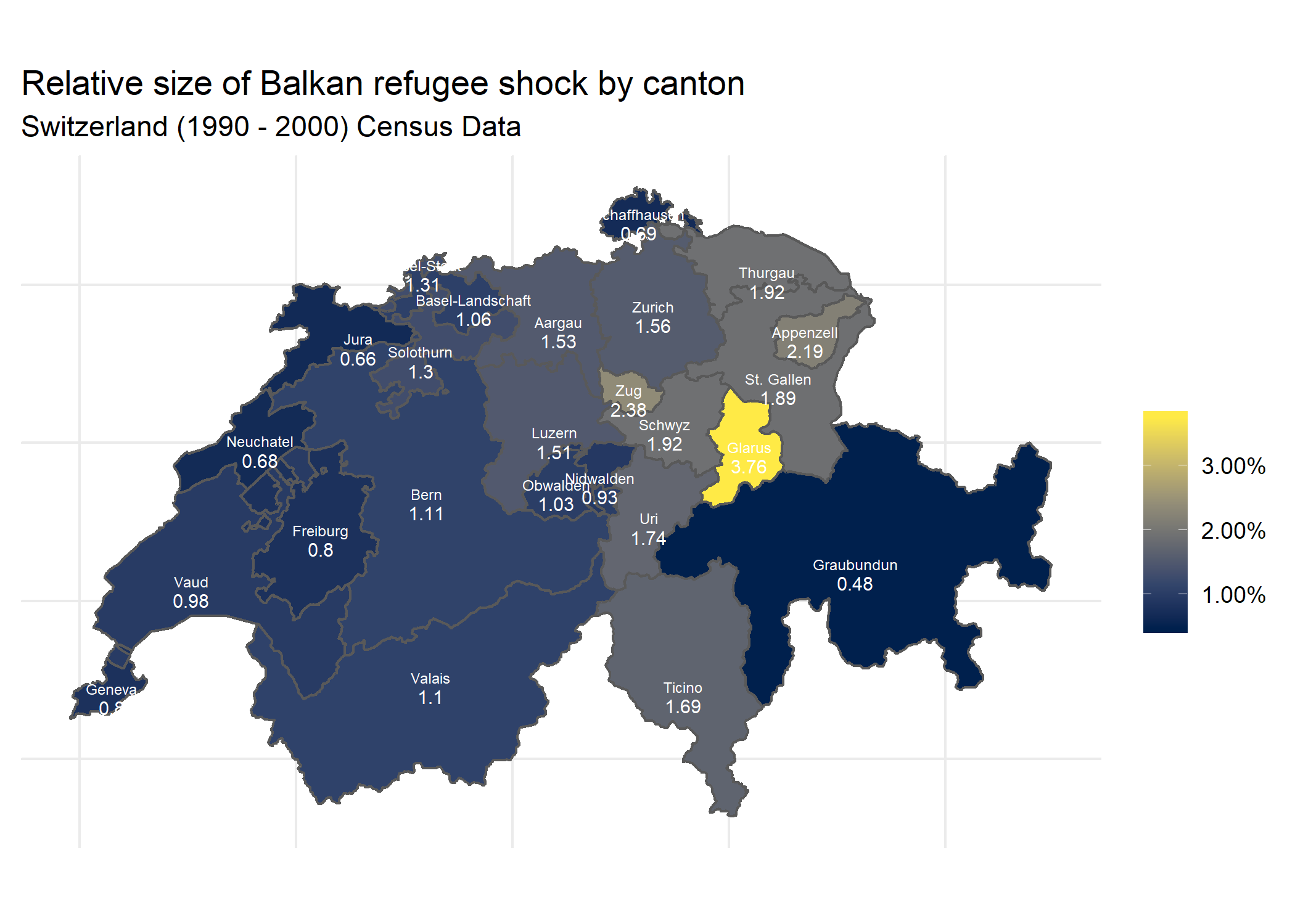
Figure 4

When we do a simple scatter plot showing the relationship between any of the labor market outcome variables and the size of the Balkan shock, we notice that: (a) there appears to be some sort of linear relationship between the two variables, (b) the direction, or sign, of this relationship is as we predicted from before, and that (c) the impact of the Balkan shock only seems to affect small cells containing workers with the lowest level of education.

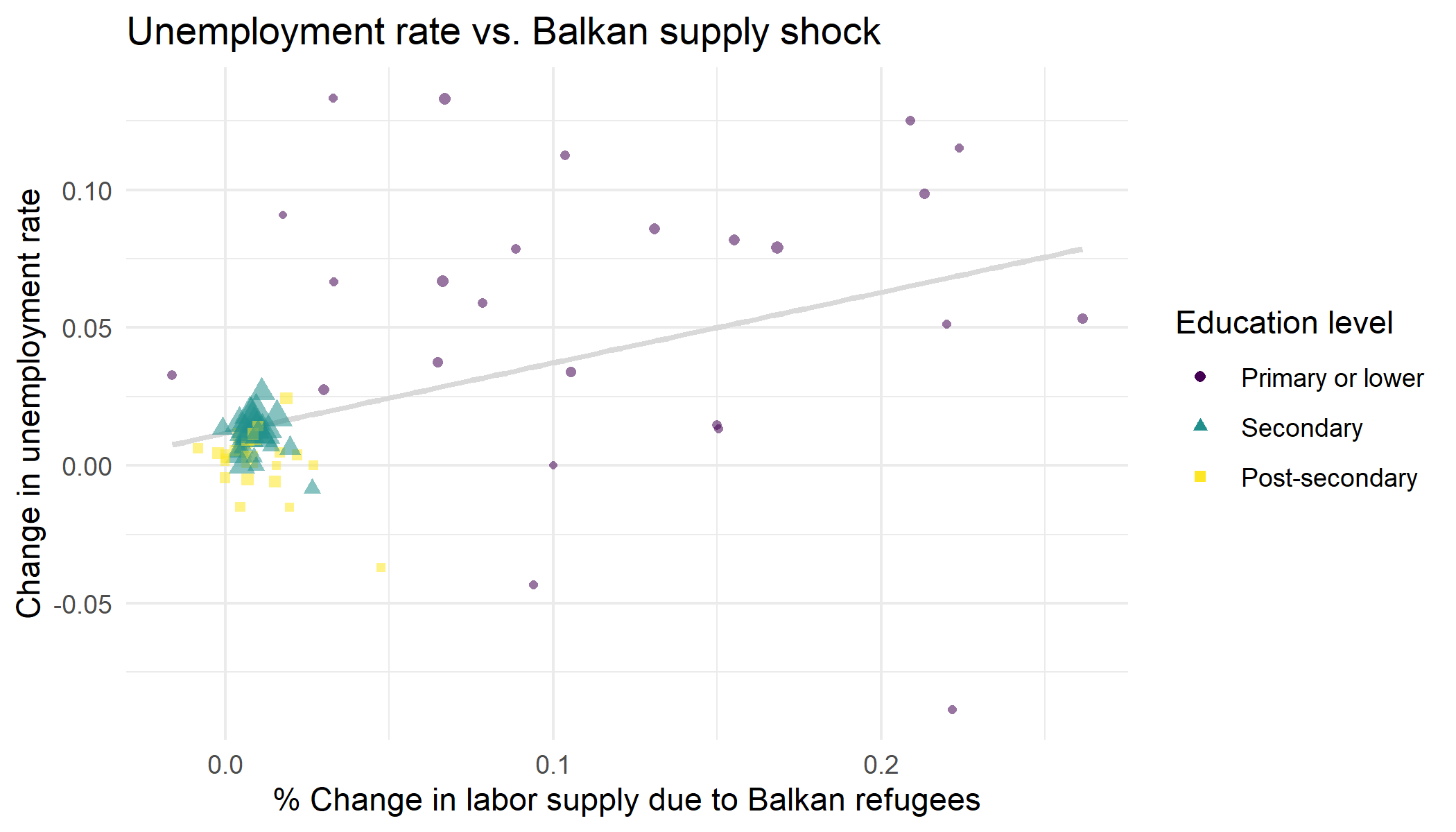
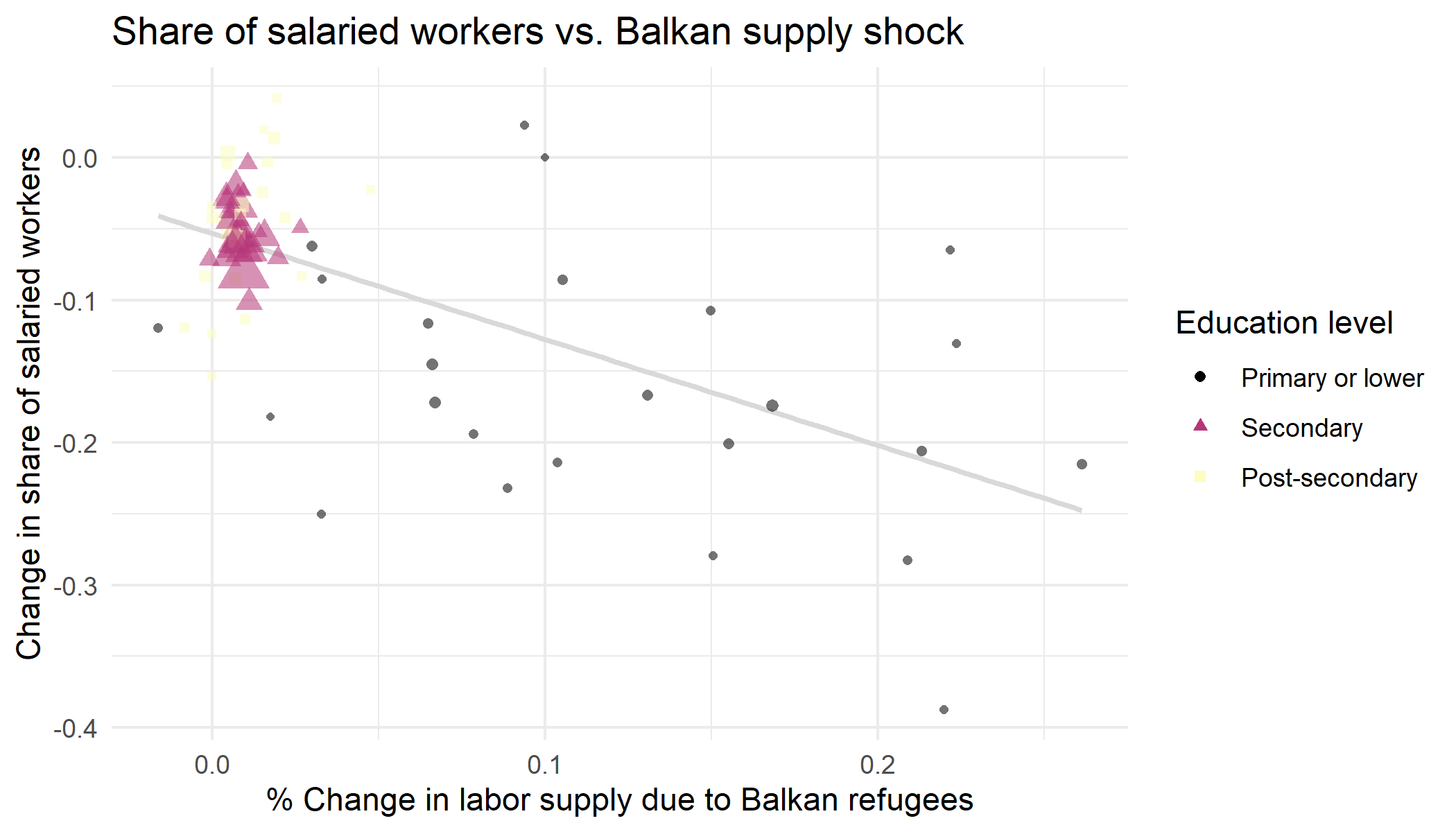
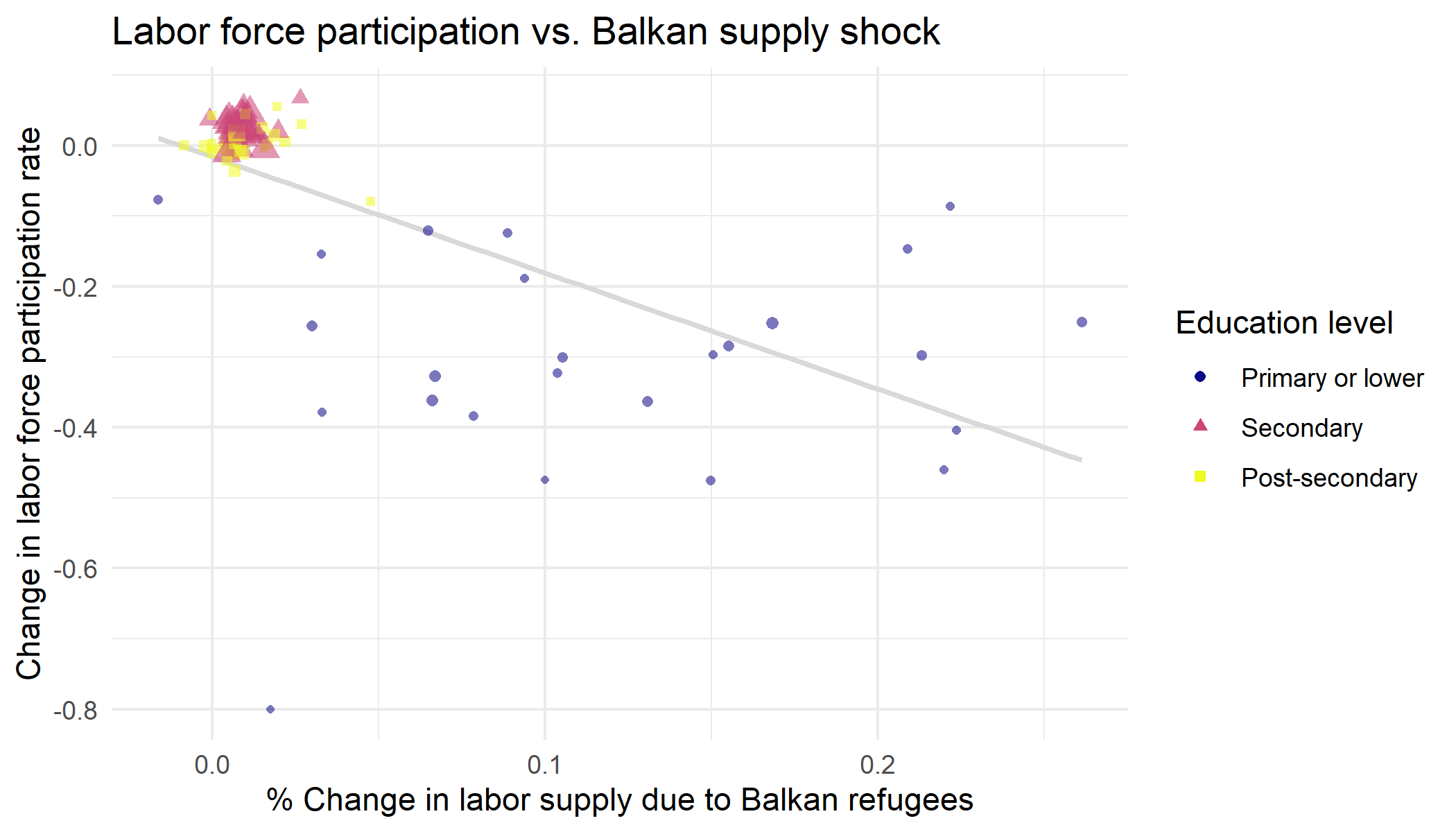
Regression results

Our assessment of the impact of refugee migration on the Swiss labor market looks at three different dependent variables: (i) the change in the unemployment rate, (ii) the change in the share of salaried workers, and (iii) the change in the share of salaried workers.

For each dependent variable, I conduct set of six regressions. I estimate (1) a baseline model with the respective dependent variable of interest regressed by the relative supply shock of Balkan migration (shock_rel), then (2) re-estimate the model controlling for the change in supply of native workers (log_nativesupp), and then (3) add a control variable for the change in the share of female workers (d_share_fem). Next, I repeat the first three regressions except I control for canton and education-level fixed effects in each (4-6).

All regressions presented here have been weighted by the size of the region-skill cell. Cell weights are calculated with \((n_0 \cdot n_1) / (n_0 + n_1)\), where \(n_0\) is the number of observations in the region-skill cell in 1990 and the \(n_1\) is the number of observations in the cell in 2000. All results are reported with Huber-White robust standard errors.

[Note: I also estimate all regressions without weights, where I find that the unweighted regressions have slightly higher precision for the fixed-effect estimations, though the signs and significance remain the same.]

Interestingly enough, for all three dependent variables, the increase in refugee immigration had a statistically significant negative effect on the corresponding labor market outcome variables, but in all cases, these effects disappeared once we controlled for region and skill fixed effects.

Below, I present a summary of the impact of the Balkan refugee shock on all dependent variables using the full model specification, controlling for region and skill fixed-effects. As we can see, no matter what controls we include in our specification, as long as we correct for fixed effects, the coefficient on our shock_rel variable is not statistically different from zero across any of the labor market outcomes of interest.

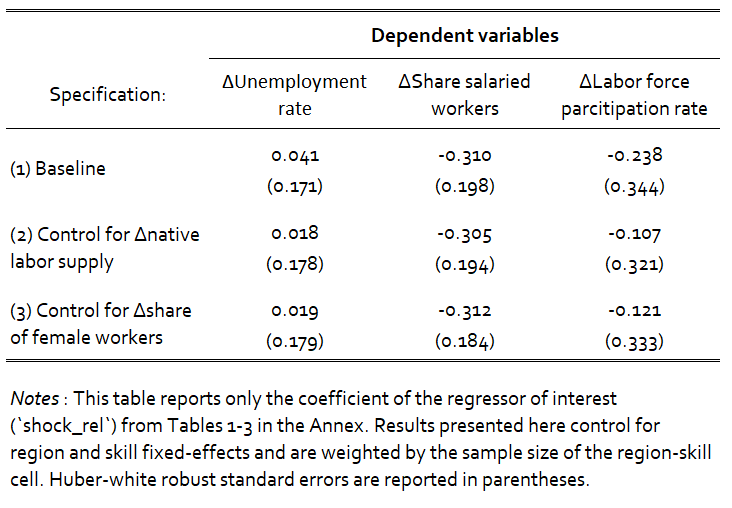
Some concluding remarks

The results from our analysis show that the impact of Balkan refugee migration to Switzerland in the 1990’s had no significant impact on the labor market outcomes for similar native workers, either in terms of their rate of unemployment, the types of work contracts they had, or their tenancy to stay in the labor force. This stands in contrast to the findings of Borjas when estimating the impact of Cuban refugees in Miami [Borjas 2003], as well as the work of Borjas and Monras when estimating the impact of refugees from Algeria in France [Borjas and Monras 2007], and when estimating the impact of Balkan refugees in Europe.

Insofar as our particular analysis is concerned, it is worth noting that estimations were also run for sub-samples including only prime-age working males (ages 25-54), as well as for sub-samples of all working age males (ages 15+), and while the more restrictive sub-sample did lead to more precise estimates, the overall pattern of the results was no different from what we find here–namely, that simple OLS estimates did show a significant negative impact of the refugee shock, but all of these effects disappeared once we control for region and skill fixed- effects.

It is worth noting that for the analysis presented here we only looked at the impact of Balkan workers on similar native workers. The approached used assumes that native and foreign workers are perfect substitutes, and ignores any cross-effects between skill groups (i.e. increased supply of low-skill workers could actually help high-skilled, or vice-versa). Additionally, we have noted that controlling for fixed effects and/or adding regression weights actually lowers the precision of our estimates. These threads are potentially worthy of further exploration, but for the moment, I will leave those questions for future follow-ups.

References